This March, I've put up two new VO resources (that's jargon for “table
or service or whatever”) that, I think, fit quite well what I like to
call tangible astronomy: things you can readily relate to what you see
when you step out at night. And, since I'm a professing astronomy nerd,
that's always nicely gratifying.
Constellations
On the constellations, you might rightfully say that's really far from
science. But then they do help getting an idea where something is, and
when and from where you might see something. I've hence wanted for a
long time to re-publish the Davenhall Constellation Boundary Data
as proper, ADQL-queriable polygons, and figuring out where the
loneliest star in the sky (and
Voyager 1) were finally made me do it.
So, since early March there's the cstl.geo table on the TAP service
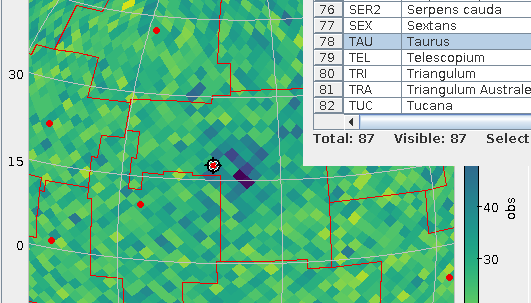
at https://dc.g-vo.org/tap with the constallation polygons in its p
column. Which, for starters, means it's trivial to overplot
constallation boundaries in your favourite VO clients now, as in the
plot above. To make it, I've just done a boring SELECT * FROM
cstl.geo, did the background (a plain HEALPix density plot of GCNS)
and, clicked Layers → Add Area Control and selected the cstl.geo table.
If you want to identify constellations by clicking, while in the area
control, choose “add central” from the Forms menu in the Form tab;
that's what I did in the figure above to ensure that what we're looking
at here is the Hyades and hence Taurus. Admittedly: these “centres“ are
– as in the catalogue – just the means of the vertices rather than the
centres of mass of the polygon (which are hard to compute). Oh, and:
there is also the AreaLabel in the Forms menu, for when you need the
identification more than the table highlighting (be sure to use a center
anchor here).
Note that TOPCAT's polygon plot at this point is not really geared
towards large polygons (which the constellations are) right now. At the
time of writing, the documentation has:
“Areas specified in this way are generally intended for displaying
relatively small shapes such as instrument footprints. Larger areas may
also be specified, but there may be issues with use.” That you'll see at
the edges of the sky plots – but keeping that in mind I'd say this is a
fun and potentially very useful feature.
What's a bit worse: You cannot turn the constellation polygons into MOCs
yet, because the MOC library currently running within our database will
not touch non-convex polygons. We're working on getting that fixed.
Nearby Stars
Similarly tangible in my book is the GCNS: nearby stars I always find
romantic.
Let's look at the 100 nearest stars, and let's add spectral types from
Henry Draper (cf. my post on Annie Cannon's catalogue) as well as the constellation
name:
WITH nearest AS (
SELECT TOP 100
a.source_id,
a.ra, a.dec,
phot_g_mean_mag,
dist_50,
spectral
FROM gcns.main AS a
LEFT OUTER JOIN hdgaia.main AS b
ON (b.source_id_dr3=a.source_id)
ORDER BY dist_50 ASC)
SELECT nearest.*, name
FROM nearest
JOIN cstl.geo AS g
ON (1=CONTAINS(
POINT(nearest.ra, nearest.dec),
p))
Note how I'm using CONTAINS with the polygon in the constellations table
here; that's the usage I've had in mind for this table (and it's
particularly handy with table uploads).
That I have a Common Table Expression (“WITH”) here is due to SQL
planner confusion (I'll post something about that real soon now): With
the WITH, the machine first selects the nearest 100 rows and then does
the (relatively costly) spatial match, without it, the machine (somewhat
surprisingly) did the geometric match first. This particular confusion
looks fixable, but for now I'd ask you for forgiveness for the hack –
and the technique is often useful anyway.
If you inspect the result, you will notice that Proxima Cen is right
there, but α Cen is missing; without having properly investigated
matters, I'd say it's just too bright for the current Gaia data
reduction (and quite possibly even for future Gaia analysis).
Most of the objects on that list that have made it into the HD (i.e.,
have a spectral type here) are K dwarfs – which is an interesting
conspiracy between the limits of the HD (the late red and old white
dwarfs are too weak for it) and the limits of Gaia (the few earlier
stars within 6 parsec – which includes such luminaries as Sirius at a
bit more than 2.5 pc – are just too bright for where Gaia data reduction
is now).
Animation
Another fairly tangible thing in the GCNS is the space velcity, given in
km/s in the three dimensions U, V, and W. That is, of course, an
invitation to look for stellar streams, as, within the relatively small
portion of the Milky Way the GCNS looks at, stars on similar orbits will
exhibit similar space motions.
Considering the velocity dispersion within a stellar stream will be a
few km/s, let's have the database bin the data. Even though this data is
small enough to conveniently handle locally, this kind of remote
analysis is half of what TAP is really great at (the other half being
the ability to just jump right into a new dataset). You can group by
multiple things at the same time:
SELECT
COUNT(*) AS n,
ROUND(uvel_50/5)*5 AS ubin,
ROUND(vvel_50/5)*5 AS vbin,
ROUND(wvel_50/5)*5 AS wbin
FROM gcns.main
GROUP BY ubin, vbin, wbin
Note that this (truly) 3D histogram only represents a small minority of
the GCNS objects – you need radial velocities for space motion, and
these are precious even in the Gaia age.
What really surprised me is how clumpy this distribution is – are we
sure we already know all stellar streams in the solar neighbourhood?
Watch for yourself (if your browser can't play webm, complain to your
vendor):
[Update (2021-04-01): Mark Taylor points out that the “flashes” you
sometimes see when the grid is aligned with the viewing axes (and the
general appearance) could be improved by just pulling all non-NULL UVW
values out of the table and using a density plot (perhaps
shading=density densemap=inferno densefunc=linear). That is quite
certainly true, but it would of course defeat the purpose of having
on-server aggregation. Which, again, isn't all that critical for this
dataset, so doing the prettier plot actually is a valuable exercise for
the reader]
How did I make this video? Well, I started with a Cube Plot in TOPCAT as
usual, configuring weighted plotting with n as its weight and played
around a bit with scaling out a few outliers. And then I saved the table
(to zw.vot), hit “STILTS“ in the plot window and saved the text from
there to a text file, zw.sh. I had to change the ``in`` clause in
the script to make it look like this:
#!/bin/sh
stilts plot2cube \
xpix=887 ypix=431 \
xlabel='ubin / km/s' ylabel='vbin / km/s' \
zlabel='wbin / km/s' \
xmin=-184.5 xmax=49.5 ymin=-77.6 ymax=57.6 \
zmin=-119.1 zmax=94.1 phi=-84.27 theta=90.35 \
psi=-62.21 \
auxmin=1 auxmax=53.6 \
auxvisible=true auxlabel=n \
legend=true \
layer=Mark \
in=zw.vot \
x=ubin y=vbin z=wbin weight=n \
shading=weighted size=2 color=blue
– and presto, sh zw.sh would produce the plot I just had in
TOPCAT. This makes a difference because now I can animate this.
In his documentation, Mark already has a few hints on how to build
animations; here are a few more ideas on how to organise this. For
instance, if, as I want here, you want to animate more than one
variable, stilts tloop may become a bit unwieldy. Here's how to give
the camera angles in python:
import sys
from astropy import table
import numpy
angles = numpy.array(
[float(a) for a in range(0, 360)])
table.Table([
angles,
40+30*numpy.cos((angles+57)*numpy.pi/180)],
names=("psi", "theta")).write(
sys.stdout, format="votable")
– the only thing to watch out for is that the names match the names
of the arguments in stilts that you want to animate (and yes, the
creation of angles will make numpy afficionados shudder – but I wasn't
sure if I might want to have somewhat more complex logic there).
[Update (2021-04-01): Mark Taylor points out that all that Python
could simply be replaced with a straightforward piece of stilts using
the new loop table scheme in stilts, where you would simply put:
animate=:loop:0,360,0.5
acmd='addcol phi $1'
acmd='addcol theta 40+30*cosDeg($1+57)'
into the plot2cube command line – and you wouldn't even need the
shell pipeline.]
What's left to do is basically the shell script that TOPCAT wrote for me
above. In the script below I'm using a little convenience hack to let me
quickly switch between screen output and file output: I'm defining a
shell variable OUTPUT, and when I un-comment the second OUTPUT, stilts
renders to the screen. The other changes versus what TOPCAT gave me are
de-dented (and I've deleted the theta and psi parameters from the
command line, as I'm now filling them from the little python script):
OUTPUT="omode=out out=pre-movie.png"
#OUTPUT=omode=swing
python3 camera.py |\
stilts plot2cube \
xpix=500 ypix=500 \
xlabel='ubin / km/s' ylabel='vbin / km/s' \
zlabel='wbin / km/s' \
xmin=-184.5 xmax=49.5 ymin=-77.6 ymax=57.6 \
zmin=-119.1 zmax=94.1 \
auxmin=1 auxmax=53.6 \
phi=8 \
animate=- \
afmt=votable \
$OUTPUT \
layer=Mark \
in=zw.vot \
x=ubin y=vbin z=wbin weight=n \
shading=weighted size=4 color=blue
# render to movie with something like
# ffmpeg -i "pre-movie-%03d.png" -framerate 15 -pix_fmt yuv420p /stream-movie.webm
# (the yuv420p incantation is so real-world
# web browsers properly will not go psychedelic
# with the colours)
The comment at the end says how to make a proper movie out of the PNGs
this produces, using ffmpeg (packaged with every self-respecting
distribution these days) and yielding a webm. Yes, going for mpeg x264
might be a lot faster for you as it's a lot more likely to have hardware
support, but everything around mpeg is so patent-infested that for the
sake of your first-born's soul you probably should steer clear of it.
Movies are fun in webm, too.

![[RSS]](../theme/image/rss.png)